تعريف معادلة برنولي هي معادلة تفاضلية عادية من المرتبة الأولى وتكتب على الشكل .

طريقة الحل:
الفكرة تكمن بتحويلها اى معادلة تفاضلية خطية من المرتبة الأولى.. ويتم ذلك من خلال الأتي..

نقوم
بالتحويلي الأتي :
 فينتج لدينا
فينتج لدينا
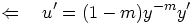 وبالتعويض بالمعادلة السابقة
ينتج لدينا المعادلة الخطية
التالية:
وبالتعويض بالمعادلة السابقة
ينتج لدينا المعادلة الخطية
التالية:

ملاحظة: يجب الأخذ
بعين الإعتبار إن كان
 حلاً أما لا وفيما إذا كان
خاص أم شاذ.
حلاً أما لا وفيما إذا كان
خاص أم شاذ.
مثال :
حل المعادلة التالية

بإستخدام
الطريقة أعلاه لدينا
 نفرض أنّ
نفرض أنّ
 وبالتالي نحصل على المعادلة :
وبالتالي نحصل على المعادلة :
[center] [/center]
[/center]
وهي معادلة
تفاضلية خطية من المرتبة
الأولى وحلها العام هو
[center] [/center]
[/center]
وبالتالي يكون لدينا
[center] [/center]
[/center]
والعلاقة الأخيرة هي الحل العام .....
ونلاحظ أنّ

هو حل للمعادلة ...ولكنه حل شاذ لانه لا ينتج من الحل العام.
فإن عدد برنولي هو صيغة رياضية كسرية لتتابع الارقام المنطقية ذات الصلة بنظرية الارقام وهي مرتبطة بدالة زيته (التي وضعها العالم الالماني ريمان) بعدد صحيح سالب. إن نظرية الارقام هي فرع من الرياضيات البحتة ويدرس الارقام بصورة عامة ويركز على الارقام الصحيحة والتمارين الرياضية المتعلقة بها. أما دالة زيته (التي وضعها العالم الالماني ريمان) فهي دالة رياضية معروفة في علم الرياضيات وذلك بسبب تأثيرها المباشر على توزيع الارقام الاولية بالاضافة الى أهمية هذه الدالة في الفيزياء ونظرية الاحتمالات والاحصاء التطبيقي. ان نظرية ريمان ( التي تتعامل مع توزيع الاصفار في الدالة ) تعتبر عند الكثير من علماء الرياضيات ومنذ عام 1732 من المسائل الرياضية غير القابلة للحل.
ولکن یبدو ان ارض السوید هي منبع الافكار الرياضية لانه كان هناك عالم للرياضيات إسمه Marcel Riesz من المجـرقد هاجر للسويد واستقر في جامعة لوند الواقعة شمال مالمو قد حاول في عام 1916 ان يحل المعادلة، وهو أخ عالم الرياضيات المشهور Frigyes Riesz. وبرغم ان Marcel Riesz قد إقترب من الحل إلا إنه لم يتمكن من تحديد قيمة عددية لرقم برنولي أو حتى قيمة دالية من أي قطع كانت حتى لو خطية.


